Skip to content

Stratifier

Warning

This library is under development, none of the presented solutions are available for download.

With this module, you can receive assistance in the stratification process of your forest plantations. Use forest inventory data to automatically stratify the plantations by selecting the forest variables you consider most relevant and either setting a predefined number of strata or allowing the module to determine the optimal number of strata.

Forest Stratification with Python

The forest stratification process requires knowledge of several factors:

  • Geographic location
  • Tree species
  • Soil type
  • Stand age
  • Product purpose
  • Management history

In this context, the Python module developed for stratification emerges as a support tool for forest planning, offering a data-driven initial perspective.

Main Functions

The module includes functions such as:

  • stratify_kmeans
  • stratify_hierarchical

These functions use multivariate clustering algorithms (k-means and hierarchical, respectively) to identify patterns in continuous variables such as:

  • Mean diameter
  • Mean height
  • Volume per hectare
  • Age
  • Site index

The algorithms group sample units into homogeneous strata, which can be used for:

  • Forest inventory
  • Sample allocation
  • Management optimization

Important

The results do not replace expert technical interpretation, but provide an objective basis for exploratory analysis, helping to support decision-making in forest projects.

Class Parameters

Stratifier

Stratifier(df, y, *train_columns, iterator=None)
Parameters Description
df The dataframe containing the forest inventory data.
*groups_columns Columns that will be used for stratification. Numeric only.
iterator (Optional) The stratification will be performed for each iterator.

Class Methods

methods and parameters
Stratifier.stratify_kmeans(k=None, k_method=None, max_k=100,
                          show_plots=True, save_plots_dir=None)#(1)!

Stratifier.stratify_hierarchical(k=None, k_method=None, max_k=10,
                                show_plots=True, save_plots_dir=None)#(2)!

  1. k = (Optional) Desired number of strata.
    k_method = (Optional) If k is not specified, which method will be used to define the number of k. Options: elbow, silhouette, davies_bouldin, calinski_harabasz. Default = "elbow".
    max_k = (Optional) Maximum number of strata to be created.
    show_plots = If true, displays the radar chart with the generated strata.
    save_plot_dir = (Optional) Directory to save the plots of the generated strata.
  2. k = (Optional) Desired number of strata.
    k_method = (Optional) If k is not specified, which method will be used to define the number of k. Options: elbow, silhouette, davies_bouldin, calinski_harabasz. Default = "elbow".
    max_k = (Optional) Maximum number of strata to be created.
    show_plots = If true, displays the radar chart with the generated strata.
    save_plot_dir = (Optional) Directory to save the plots of the generated strata.
Methods Description
.stratify_kmeans() Performs stratification using the K-Means algorithm.
.stratify_hierarchical() Performs stratification using the Agglomerative Clustering algorithm.

Important

When the variable k is not defined, the algorithm will attempt to automatically determine the optimal number of strata using the elbow method by default.

To choose a different method for automatic k selection, simply provide the method parameter with the desired method name. The available methods are:

  • elbow: Based on inertia analysis for different k values. Uses the second derivative to identify the inflection point.
  • silhouette: Uses the silhouette coefficient to evaluate group separation. Higher values indicate better clustering.
  • davies_bouldin: Assesses group compactness and separation. The lower the index, the better the clustering.
  • calinski_harabasz: Uses the ratio between inter-cluster dispersion and intra-cluster dispersion. The higher the index, the better the clustering.

Each method adapts better to different data characteristics. Choosing the appropriate one can significantly improve the quality of the generated strata.

Likewise, users can limit the maximum number of strata through the max_k variable, which sets the highest k value to be considered during the automatic evaluation process.

Example Usage

As an example, we will use an adapted dataset from Arce and Dobner Jr. (2024) for Eucalyptus dunnii. The dataset consists of 81 plots of 300 m², all with an age of 7 years.

Download the file.

stratifier_example.py
1
2
from fptools.stratifier import Stratifier#(1)!
import pandas as pd#(2)!

  1. Import the Stratifier class.
  2. Import pandas for data manipulation.

stratifier_example.py
 3
 4
 5
 6
 7
 8
 9
10
11
12
df = pd.read_excel(r'C:\Your\path\dados_stratifier.xlsx')#(1)!

columns_to_check = [
    'Idade', 'N_ha', 'd', 'h', 'Hdom',
    'G_m2_ha', 'V_m3_ha',
]#(2)!

st = Stratifier(df, *columns_to_check)#(3)!

stratified_df = st.stratify_kmeans(save_plots_dir=r"Your\path\to\save\plots")#(4)!

  1. Load your xlsx file containing the inventory data.
  2. Create a list called columns_to_check containing the columns to be used for stratification.
  3. Create the variable st using the df dataframe, passing the columns_to_check as stratification parameters.
  4. Perform stratification using the "KMeans" algorithm, allowing the algorithm to determine the number of strata. Save the results in the stratified_df variable. Save the generated radar chart in the specified directory.

Outputs

Tables

stratified_df (1)

  1. Initial DataFrame with an additional column called Cluster, which contains the cluster number assigned to each data row, ranging from 0 to n.
Chave_Parcela Idade N_ha d h Hdom G_m2_ha V_m3_ha S Cluster
14401109002_P1 7 866.67 16.63 16.09 16.50 19.43 112.77 15.44 0
14401109003_P2 7 866.67 16.55 15.02 16.47 19.91 110.36 15.17 0
14401110009_P3 7 600.00 16.96 14.07 15.32 13.92 64.83 14.71 0
1440817_P3 7 1066.67 16.45 14.53 16.49 24.24 129.46 14.61 0
1440818_P6 7 833.33 17.27 14.62 16.00 20.79 112.73 12.64 0

Charts

Example of a radar chart generated by the `stratify_kmeans` method. The chart shows the normalized mean of each variable for each cluster.
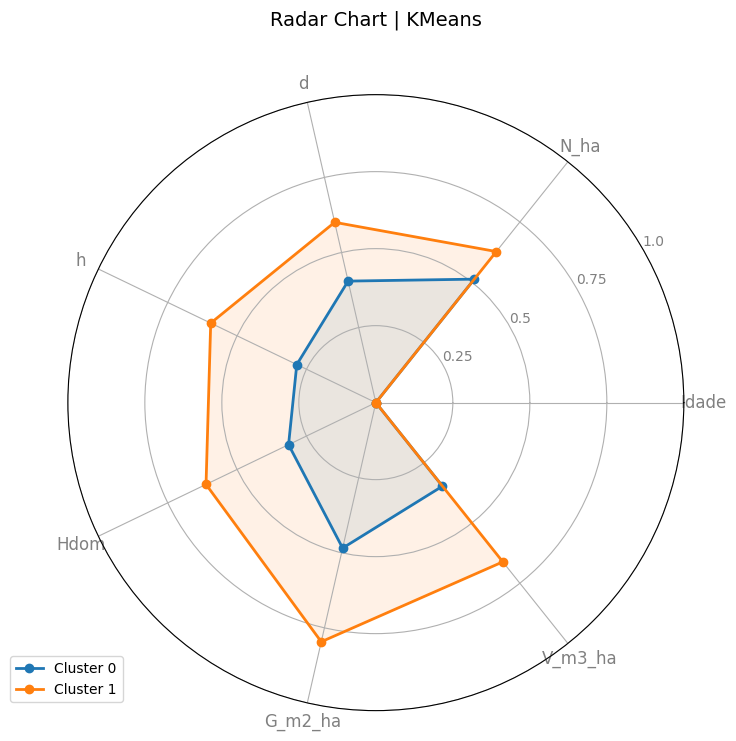
Plugin interface

References

ARCE, JULIO EDUARDO; DOBNER JR., MARIO. (2024). Management and planning of planted forests: with emphasis on the Pinus and Eucalyptus genera. Curitiba, PR: Ed. dos Autores, 419p.

KARCZMAREK, Pawel; KIERSZTYN, Adam; PEDRYCZ, Witold; AL, Ebru. K-Means-based isolation forest. Knowledge-Based Systems, Amsterdam, v. 195, p. 105659, May 11, 2020. Available at: https://doi.org/10.1016/j.knosys.2020.105659. Accessed on: May 22, 2025.

DETRINIDAD, E.; LÓPEZ-RUIZ, Víctor-Raúl. The Interplay of Happiness and Sustainability: A Multidimensional Scaling and K-Means Cluster Approach. Sustainability, v. 16, n. 22, p. 10068–10068, November 19, 2024.

MÄRZINGER, T.; KOTÍK, J.; PFEIFER, C. Application of Hierarchical Agglomerative Clustering (HAC) for Systemic Classification of Pop-Up Housing (PUH) Environments. Applied Sciences, v. 11, n. 23, p. 11122, November 24, 2021.